斐波那契数列

转至：https://blog.csdn.net/IronWring_Fly/article/details/100050016

斐波那契数列来源于兔子繁殖问题，所以也叫兔子序列。

tqmeyI4ZKWGlbOr.jpg

最开始我一直不能理解兔子问题怎么和斐波那契数列联系在一起的，然后画了这个图之后，就明白了。
第一年有一对小兔子，一年后成年。成年的兔子又可以生出一对小兔子，如此循环往复，每年的兔子数就构成了一个斐波那契数列。
斐波那契数列有很多马甲：

• 爬楼梯问题，一次可以爬一级，也可以爬两级；
• 用1个2 * 1个小矩形覆盖8个2*1的小矩形问题（剑指offer）。

四种解决方法

1. 递归

这是最简单，也是效率最差的一种：

public long recursive(int n) {
        if (n <= 0) return 0;
        if (n == 1) return 1;
        return recursive(n - 1) + recursive(n - 2);
    }

• 时间复杂度指数级，他的递归通项公式可以转换为一个齐次二阶常系数差分方程：
• 设f(n)为参数为n时的时间复杂度，很明显：f(n)=f(n-1)+f(n-2) ，且f(0)=0; f(1)=1;
• 特征方程为：x^2-x-1=0
  • 得 x=(1±√5)/2
  • 因而f(n)的通解为:

2Zkl1JKI6GteE4P.png

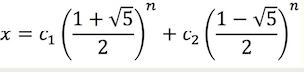
• 由f(0)=0; f(1)=1可解得c_1，c_2
  • 最终可得，时间复杂度为：

iZfNLuArEIFaJB8.png

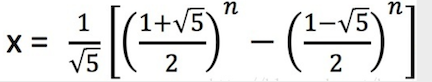
真是没想到，高数里的差分方程在这里用到了，说真的，我刚看到这里还挺惊喜的。

2. 数学公式法

有了上述时间复杂度的分析，就可以直接套用最后得出的公式，直接利用给的n计算x，时间复杂度O（logn）。因为涉及到幂运算。

3. 动态规则

利用动态规划的思想，利用递归分析问题，找到状态转移方程，然后从第一个状态开始迭代到最终状态。

• 这里的状态转移方程是：f(n) = f(n - 1) + f(n - 2)   (n > 2)
  • 初始状态：f(0) = 0; f(1) = 1;

public long addition(int n) {
        int[] result = {1, 2};
        if (n < 2) {
            return result[n];
        }
        long n1 = 0;
        long n2 = 1;
        long n3 = 0;
        for (int i = 2; i <= n; i++) {
            n3 = n1 + n2;
            n1 = n2;
            n2 = n3;
        }
        return n3;
    }

4. 矩阵乘法

BNvjJ52R9fotxCG.jpg

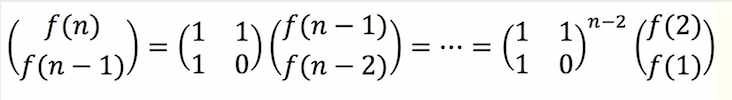
let matrix22_mul = (x, y) = >{
	[x[0][0] * y[0][0] + x[0][1] * y[1][0], x[0][0] * y[0][1] + x[0][1] * y[1][1],
	 x[1][0] * y[0][0] + x[1][1] * y[1][0], x[1][0] * y[0][1] + x[1][1] * y[1][1]]
}
let matrix22_pow = (x, n) =>{
	var r = [[1,0],[0,1]];
	var v = x;
	while (n) {
		if (n % 2 == 1) {
			r = matrix22_mul(r, v);
			n -= 1;
		}
		v = matrix22_mul(v, v);
		n = n / 2;
	}
	return r;
}
let fibnacci = n => n <= 0 ? 0 : 
				    matrix22_mul([[0,1],[0,0]], matrix22_pow([[0,1],[1,1]], n - 1))[0][1];

看到winter大神写的代码，待我理解理解后面转为java，再来修改。